uma introdução amigável a Monte Carlo Tree Search (usando jogo da velha)

introdução

Monte Carlo Tree Search, ou MCTS, é um algoritmo utilizado para fazer busca em árvores que são particularmente grandes. Ao empregar a "aleatoriedade direcionada" comum aos métodos de Monte Carlo, o algoritmo resolve algumas das dificuldades inerentes ao percurso de árvores com muitos nós. O objetivo desse texto é dar uma introdução amigável ao assunto, sendo bem explícito em pontos que talvez façam algumas pessoas tropeçarem (como eu certamente tropecei).

Em que situações um algoritmo como o MCTS é bem-vindo? Uma das aplicações mais famosas é na área de inteligência artificial para jogos. Nessa área, é comum ter como objetivo a tarefa de "buscar a melhor jogada, dentre todas as jogadas possíveis". Esse problema em si já é uma busca, mas se representarmos todas as decisões possíveis do jogo como uma árvore, o problema acaba virando especificamente uma busca em árvore. Por exemplo:

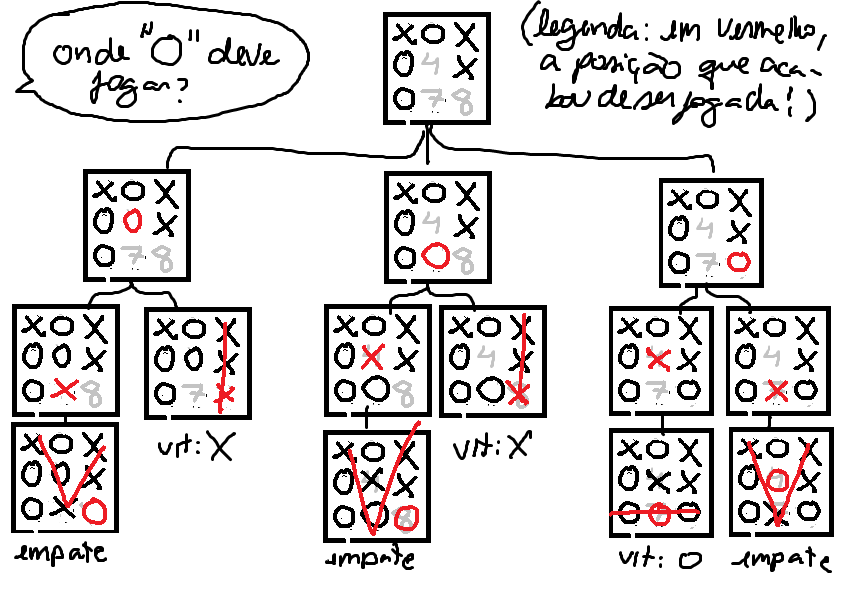
Para decidir em que posição jogar, o jogador O deve considerar qual posição irá aumentar suas chances de vencer. Nós sabemos que a jogada "O8" é a melhor, mas como o agente descobriria isso olhando apenas para a árvore de jogo? Ele teria de expandir essa árvore e observar que quando ele joga nessas posições, há mais possibilidades de vitória. Em outras palavras, ele teria de buscar na árvore as decisões que lhe trazem mais vitórias.

O jogo da velha é um caso trivial: são apenas 9 espaços, e a cada turno o jogador tem menos decisões possíveis pra analisar. Nesse caso, é factível construir uma árvore com todos os tabuleiros possíveis, e simplesmente consultar ela toda vez que formos fazer uma jogada. Mas e em um jogo como Pacman, onde a todo frame o jogador pode selecionar uma de 4 direções, e demora milhares de frames até que o fim do jogo seja alcançado? Nesse caso, construir a árvore completa não é tão factível assim!

Felizmente, o que o MCTS nos permite fazer é justamente obter uma boa decisão sem ter que expandir a árvore inteira. A gente vai analisar ele no caso do jogo da velha porque é mais simples, mas vai ficar claro que ele pode ser aplicado em outras situações, desde que façamos uma modelagem adequada.

funcionamento

De forma bem informal, o que o algoritmo faz é muito parecido com o que muitos de nós fazemos enquanto estamos pensando na próxima jogada: analisar aos poucos a árvore de jogo procurando as decisões mais promissoras. É como se ele estivesse falando: "eu posso botar um X aqui, mas aí ele vai marcar um O aqui, e aí eu vou perder... então é melhor eu não botar o X aqui... onde eu boto então? vamos supôr que eu bote aqui..." e assim por diante. Basicamente, ele vai continuar fazendo isso até atingir algum gatilho que nós escolhemos - como um tempo máximo de execução, ou um número fixo de iterações.

O mais importante de entender de cara é que o objetivo do algoritmo é construir uma árvore de jogo. A cada iteração ele vai botar um nó novo na árvore, referente a uma decisão que pode ser tomada em algum momento do jogo (p.ex.: "jogador 1 bota X na posição 7"). O segredo é que o MCTS vai focar a construção nos caminhos que contém as decisões mais promissoras.

Mas o que significa uma decisão ser promissora? Significa duas coisas diferentes:

tomar essa decisão agora levará a mais vitórias no futuro (ela é uma boa decisão), ou
essa decisão não foi analisada muito a fundo (ela tem potencial inexplorado).

Esses vão ser os dois fatores analisados na hora de escolher qual decisão será expandida (existe uma forte similaridade com a ideia de exploration vs. exploitation discutida em outros contextos).

Mais especificamente, cada nó de decisão possui dois atributos:

valor: um número que representa o quão atrativa é aquela decisão. Um valor alto significa que a decisão é boa.
- no exemplo do jogo da velha, podemos modelar isso como o saldo de vitórias atingidas caso o jogador tome essa decisão. Por exemplo, se uma vitória vale $+1$ , um empate vale $0$ e uma derrota vale $-1$ , evidentemente uma decisão boa teria um saldo positivo e uma decisão ruim teria um saldo negativo.
visitas: um número que representa quantas vezes aquela decisão já foi analisada. Se um nó tiver um número de visitas baixo (quando comparado ao resto da árvore, claro), significa que não demos muita atenção àquela decisão: isto é, ela tem potencial inexplorado.

Uma coisa importante de notar nessa nossa modelagem do jogo da velha é que o atributo valor tem de obrigatoriamente ser relativo a um jogador. Afinal, pra dizermos se uma decisão é boa, precisamos saber: boa pra quem? Uma decisão que é boa pra mim não é boa pra você, meu adversário. Portanto, nessa modelagem, cada nó de decisão deve ter atrelado a si mesmo um jogador. Observe a seguinte situação: vamos supôr que eu (jogador X) estou jogando contra você (jogador O), e você está usando o algoritmo do MCTS pra decidir como atuar. Digamos que você está prestes a ganhar o jogo:

Existem várias decisões que eu posso tomar a partir desse momento. Qual delas é a melhor? Pra mim, é bloquear a sua vitória! Portanto, o nó de valor mais alto é justamente o nó em que eu faço isso (X7), apesar de ser você que está rodando o algoritmo.

Mas por que isso é relevante? Quando olharmos o algoritmo em si isso vai ficar mais claro, mas podemos fazer um argumento intuitivo: se o o algoritmo sempre atribuísse o valor do nó referente ao jogador inicial, ele estaria implicitamente dizendo que as partes da árvore em que o jogador adversário "deixa ele ganhar" são mais promissoras. E isso não é muito útil na realidade, porque faria o algoritmo ser muito otimista! É como se ele estivesse pensando: "eu vou botar um X aqui e aí só falta mais um pra eu ganhar! bom, ele pode me bloquear botando um O aqui, é claro. mas ele provavelmente não vai fazer isso, porque ele também quer que eu ganhe! então vou botar um X aqui mesmo". É fofo, mas irreal. O mundo é cruel, algoritmo...

A única coisa que faz sentido é esperar que os seus adversário joguem contra você, e portanto explorar a árvore levando isso em consideração. Não só no jogo da velha, mas em qualquer jogo com dois ou mais jogadores.

Voltando. A essa altura do campeonato é importante deixar claro que existem diversas variações pro algoritmo MCTS, e a que vamos abordar é uma das mais "padrão". Nessa nossa abordagem, uma decisão é determinada promissora de acordo com a seguinte fórmula, denominada UCT (Upper Confidence Bound for Trees):

$UCT = \underbrace{\frac{Q(i)}{N(i)}}_{\text{boa decisão}} + \underbrace{\sqrt{\frac{2 \ln N(j)}{N(i)}}}_{\text{decisão com potencial inexplorado}}$

tal que:

$j$ é o pai do nó $i$ ;
$Q(i)$ é o valor do nó $i$ ;
$N(i)$ é a quantidade de visitas do nó $i$ .

Analisando com mais carinho, observamos que:

o primeiro termo, $\frac{Q(i)}{N(i)}$ , calcula o "valor médio" do nó $i$ , dividindo seu valor pela quantidade de visitas - se ele teve muitas visitas com valor alto, esse valor médio também será alto. Portanto, ele está relacionado com a nossa noção de boa decisão.
o segundo termo, $\sqrt{\frac{2 \ln N(j)}{N(i)}}$ , utiliza as visitas do nó $i$ em relação às visitas de seu pai, para retornar um valor alto quando a quantidade de visitas do nó $i$ for baixa em relação às do seu pai (p. ex.: seu pai foi visitado 100 vezes mas o nó $i$ foi visitado apenas 2. isso retornaria um valor mais alto do que o dos irmãos de $i$ ).

Estudar a razão particular pra fórmula ser desse jeito foge do escopo desse texto, mas ela pode ser conferida aqui. Ter uma noção das suas componentes e do que elas medem já é suficiente pra entender o funcionamento do algoritmo. Vamos logo falar de como ele funciona.

etapas

O algoritmo pode ser dividido em 4 etapas:

seleção
expansão
simulação
retropropagação

Pra acompanhar esse texto, temos uma página na qual você pode jogar contra o MCTS, e observar a árvore sendo construída passo-a-passo. Certamente você não entenderá tudo - afinal, não falamos sobre as etapas ainda -, mas vale a pena deixar aberto e ir dando uma olhada conforme lê, pra enriquecer sua compreensão dos exemplos.

1. seleção

"Qual a decisão mais promissora a ser analisada?"

Na etapa de seleção, o algoritmo vai partir da raiz e percorrer a árvore descendo pelos nós de maior UCT, até chegar em um nó que satisfaça uma das seguintes 2 condições:

o nó ainda pode ser expandido, ou
o nó é um estado terminal (vitória, derrota ou empate).

Só isso!

Pra entender o motivo por trás dessa etapa, primeiro precisamos entender o que significa "poder ser expandido".

Um nó "pode ser expandido" quando existem jogadas imediatas a partir dele que ainda não foram incluídas na árvore. Em outras palavras: ainda existem filhos possíveis que ele não tem. Observe na árvore abaixo:

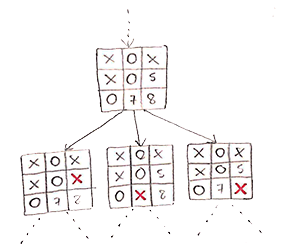
O nó "O4" ainda pode ser expandido porque a jogada "X8" é possível mas não está na árvore. Em contrapartida, o nó "X0" não pode mais ser expandido, dado que todas as jogadas possíveis a partir dele já estão incluídas na árvore - no caso, nenhuma jogada a partir dele é possível, já que o jogo acabou assim que X venceu. Mais formalmente, "X0" é um nó terminal, e portanto jamais pode ser expandido.

Ok, agora que tiramos isso do caminho, podemos voltar: qual é o intuito da etapa de seleção? A resposta pra isso é simples, se você lembrar que estamos tentando construir uma árvore! A etapa de seleção simplesmente seleciona um nó com filhos que ainda não foram construídos, para que possamos construí-los nas etapas seguintes. E qual o critério de seleção que estamos usando? O UCT, que representa a promessa de cada nó. Uma imagem para ilustrar o que está acontecendo:

Por isso estamos de olho em nós que ainda podem ser expandidos - por definição, eles são partes ainda não construídas da nossa árvore.

Mas espera. "Ainda poder ser expandido" é só uma das condições de parada da etapa de seleção! A outra é "ser um estado terminal". Por que precisamos ficar atento também a essa segunda condição? Isso é simplesmente para considerar a seguinte situação:

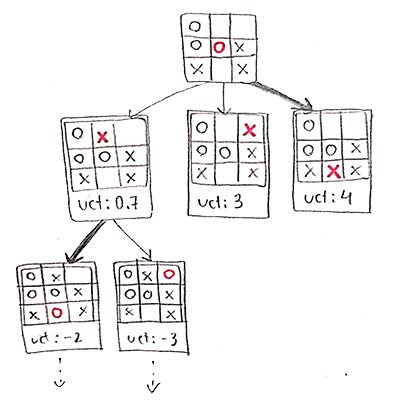
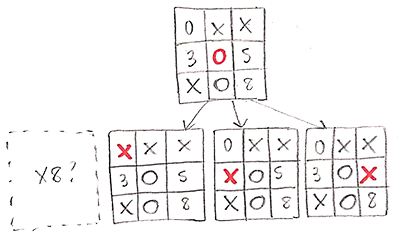
Nesse caso, o nó "X7" foi selecionado, porém ele é terminal e não pode mais ser expandido! Ao invés de rodarmos a etapa novamente (e obter o mesmo resultado, já que não há aleatoriedade envolvida), simplesmente retornamos "X7" mesmo e pulamos a etapa de expansão, indo direto para a etapa de simulação.

2. expansão

"Adicione um novo nó na árvore"

Na etapa anterior, selecionamos o nó mais promissor que ainda pode ser expandido. Agora, vamos adicionar seus nós filhos à árvore.

Existem diversas formas de fazer isso, e essa é uma decisão de design do algoritmo. Um método possível é escolher aleatoriamente um dos filhos possíveis e adicioná-lo à árvore. Outro é adicionar todos os filhos possíveis simultaneamente. Uma figura pra ilustrar as diferenças:

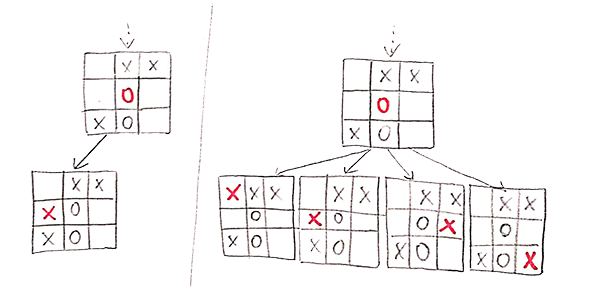
Independente de qual for o método de expansão escolhido, no fim a etapa fará sempre a mesma coisa: adicionar nós à árvore.

3. simulação

"Qual o valor desse nó expandido?"

Então chegamos na etapa de simulação. Ela é o coração do MCTS, e é de longe a etapa mais complicada. Aguenta firme que vai dar tudo certo.

Existem dois tipos de situação em que essa etapa começa.

o nó atual é um nó recém-expandido, ou
o nó atual é um nó terminal (a etapa de expansão foi pulada).

Por enquanto a gente vai se focar no primeiro caso, e inevitavelmente a gente vai acabar entendendo o segundo.

Pois bem. Acabamos de inserir um novo nó na nossa árvore. Agora, precisamos inicializar seus atributos valor e visitas. O atributo visitas é fácil: a gente inicializa ele com $1$ que é a nossa visita atual. Mas e o atributo valor? Como a gente calcula ele, de fato?

Já mencionamos que o valor de um nó está relacionado à ideia de saldo de vitórias, ou seja, um esquema parecido com o seguinte:

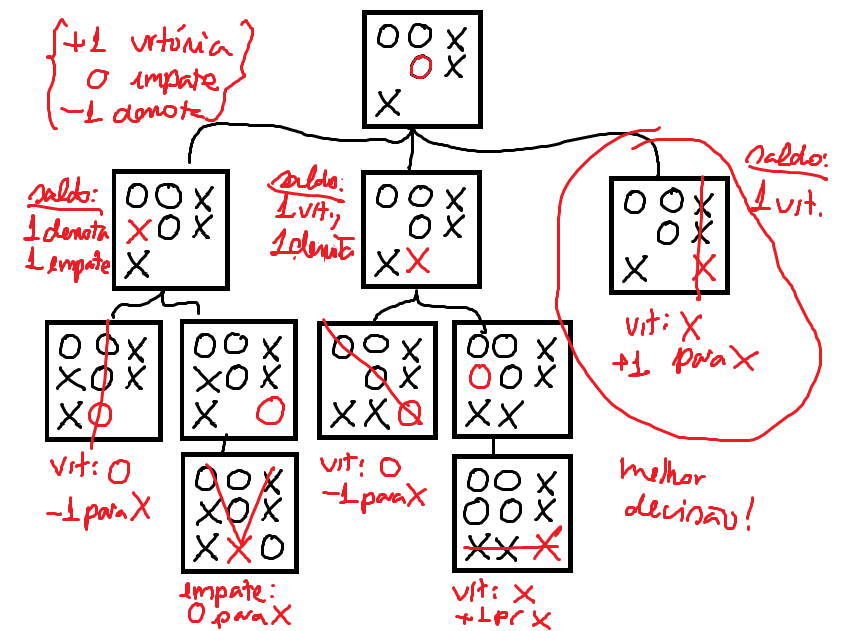
Nesse caso, teríamos de dar um peso para cada resultado para definir qual a melhor decisão. Se dermos $+1$ para vitórias, $0$ para empates e $-1$ para derrotas, então a melhor decisão seria X8. Mas se por algum motivo determinarmos que uma derrota valeria $0$ ... então nesse caso X8 estaria empatado com X7. Em resumo: não depende só do saldo de vitórias e derrotas, mas também de como pesamos cada um desses resultados.

Tendo isso em mente, a pergunta de "como inicializar o atributo valor" parece meio estúpida. Se queremos saber o valor do nó $N$ , é só contar todos os nós terminais na sub-árvore de raiz $N$ , e utilizar nosso esqueminha pra calcular o saldo do nó $N$ !

Tudo muito bom, tudo muito certo. Só tem um problema: a gente não tem a sub-árvore! A gente partiu do pressuposto de que a árvore é gigantesca e que não é conhecida a priori. Então, "contar os nós terminais" é simplesmente impossível!

Mas se a gente não consegue fazer isso, a gente vai fazer o quê então?

(Entra Monte Carlo.)

[aside: Métodos de Monte Carlo]

Métodos de Monte Carlo são amplamente utilizados pra calcular valores que não podemos conhecer com exatidão. Eles funcionam basicamente da seguinte forma:

Suponha que eu te dou uma moeda não-viciada, e peço pra você jogá-la 2 vezes. Já que a moeda é não-viciada, será que vai dar 1 cara e 1 coroa? Claro que não! Há uma chance razoável de dar 2 caras ou 2 coroas. Falando em termos de fração, é altamente possível que a fração de caras dê algo diferente de 1/2, assim como a fração de coroas.

Agora, suponha que você jogue essa moeda 100 vezes. Será que ela vai dar exatamente 50 caras e 50 coroas? Muito provavelmente também não. Mas é muito mais improvável que dê 100 caras e 0 coroas! Ou seja, a fração de caras obtida certamente não será exatamente 1/2, mas será algo muito mais próximo disso do que no caso em que jogamos a moeda apenas 2 vezes.

Se estendermos esse argumento pra números cada vez maiores, a conclusão que podemos chegar é: quanto mais vezes jogamos a moeda, maior é a chance da fração de caras obtida se aproximar da probabilidade real da moeda. Essa é a chamada lei dos grandes números.

Nesse caso, você sabia qual era a probabilidade da moeda dar cara (já que ela é não-viciada). Mas e se eu te desse uma moeda viciada, e pedisse pra você descobrir qual é a sua probabilidade? Nesse caso, você poderia fazer a mesma coisa. Você poderia jogar a moeda um montão de vezes, e observar a fração de vezes em que ela dá cara. Se você jogar 10.000 vezes e der 7.000 caras, um bom chute seria que a moeda dá cara com probabilidade 7/10.

Esse é o princípio dos métodos de Monte Carlo: amostrar aleatoriamente de uma distribuição muitas vezes, e observar a fração dos resultados obtidos. Essa fração vai se aproximar bastante da fração real desejada, quanto mais amostras tivermos.

Como vamos aplicar Monte Carlo especificamente no algoritmo MCTS?

Pra estabelecer isso, precisamos definir duas coisas:

a quantia que queremos estimar, e
o que será nossa amostra aleatória.

A quantia que queremos estimar é fácil: é o saldo de vitórias, ou melhor dizendo, a quantidade de vitórias, derrotas e empates a partir de uma determinada decisão. Na verdade, a gente se satisfaz com a fração de vitórias, derrotas e empates - p. ex.: não é muito diferente pra nós saber se há "2 vitórias, 3 derrotas e 1 empate" ou se "há 2/6 de vitórias, 3/6 de derrotas e 1/6 de empate". Em ambos os casos, fica claro que o resultado mais frequente é derrota, e é isso que importa pra gente.

Então o primeiro ponto já está definido. Mas o que seria nossa amostra aleatória?

No exemplo de cara ou coroa, queríamos estimar a fração de caras e coroas, e portanto nossas amostras aleatórias eram elementos $\text{(cara)}$ ou $\text{(coroa)}$ . No MCTS será idêntico: queremos estimar a fração de vitórias, derrotas e empates e nossas amostras aleatórias vão ser elementos $\text{(vitória)}$ , $\text{(derrota)}$ ou $\text{(empate)}$ . Em outras palavras, vamos amostrar aleatoriamente resultados possíveis a partir de uma decisão.

Como isso se dá de fato? Através de uma simulação. Nós simplesmente simulamos jogadas aleatórias a partir do tabuleiro atual até chegar em um resultado. Esse será nosso resultado aleatório, e nos dará uma informação de (vitória), (derrota) ou (empate). Pra ilustrar:

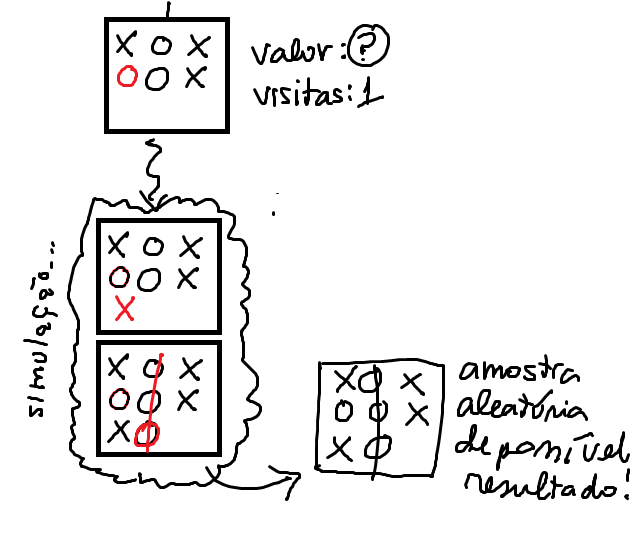
E é basicamente isso que vamos fazer na etapa de simulação! Amostrar aleatoriamente um possível resultado a partir de um nó.

[aside: aheurístico]

Mas espera. Isso parece horrível! Se a gente considerar o comportamento de todos os jogadores como aleatório, vamos acabar chegando em resultados que são possíveis, mas certamente não são plausíveis. Por exemplo, vamos dar uma olhada no exemplo acima.

Nesse caso, é claro que o jogador X pode fazer a jogada X6, mas ele certamente não fará isso porque se botar em X8 ele ganha! Então apesar de X6 ser uma jogada possível, sabemos que ela nunca aconteceria na vida real (de novo, o argumento sobre a crueldade do mundo). Certamente deveríamos considerar esse tipo de informação na hora de fazer as nossas simulações!

E de fato, isso é verdade. Podemos aprimorar nossas simulações com heurísticas, pra melhor modelar o comportamento de cada um dos jogadores. Mas o ponto crucial de se entender aqui é que o algoritmo funciona sem isso. Ou seja, mesmo se nenhuma heurística for providenciada para o MCTS, ele é capaz de estimar as melhores jogadas com base no horizonte de possibilidades.

Isso significa que o algoritmo pode acabar fazendo jogadas sub-ótimas de vez em quando (ou de vez em muito, dependendo das características do jogo e dos jogadores). Mas em tese, ele funciona. E por isso ele é chamado de um algoritmo aheurístico (isto é, ausente de heurísticas).

Então, pra calcular o valor do nó $N$ a gente vai amostrar aleatoriamente resultados possíveis do jogo a partir do tabuleiro de $N$ , e fazer isso milhares de vezes para obter uma boa estimativa. É isso?

Hum... mais ou menos.

Tem duas "pegadinhas" aqui: uma sobre consequências e outra sobre quantidade.

A primeira pegadinha é que quando obtemos alguma informação sobre um nó, estamos indiretamente obtendo informações sobre seus antecessores. Por exemplo: se a jogada X7 nos leva a muitas derrotas, não significa só que X7 é uma jogada ruim, mas também que a jogada anterior provavelmente não foi muito boa, e que a anterior também, e assim por diante. Ou seja, ao amostrarmos aleatoriamente um resultado possível a partir de um nó, estamos estimando não só o seu saldo de vitórias, como também o saldo de vitórias de todos os seus antecessores. Por isso, precisaremos retropropagar o resultado da simulação, que é o que faremos na etapa seguinte. Vale a pena enfatizar: a simulação de um nó também é, de certa forma, uma simulação de seus antecessores.

A segunda pegadinha é que, ao inicializar um nó, não vamos gerar milhares de amostras para obter uma estimativa do saldo. Na verdade, nesse primeiro momento, vamos gerar apenas uma amostra!

Não, peraí, como assim? O ponto não era gerar milhares de amostras justamente para obter uma boa estimativa do saldo? Então por que apenas uma?

Porque na verdade o que vamos fazer é o seguinte: vamos amostrar seu valor uma vez na inicialização, e mais vezes se ele for promissor.

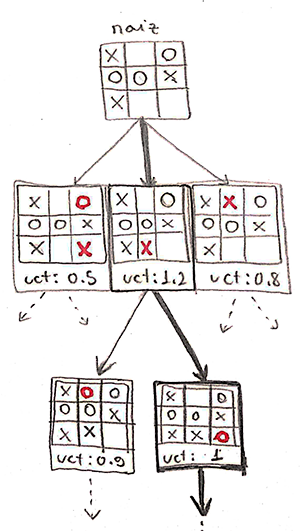
Então por exemplo. Vamos supôr que a gente selecionou um nó $N$ , expandiu ele, e agora fez uma simulação pra descobrir o valor do nó recém-expandido $M$ . Vamos supôr que essa simulação resultou em vitória. Isso significa que o nó $M$ é uma ótima decisão? Não, porque podemos ter dado sorte - uma única amostra aleatória não é uma boa estimativa do valor real. Mas é um indício! E se esse for o melhor indício que tivermos até agora, então o UCT do nó $M$ será alto, e ele provavelmente será selecionado em alguma iteração futura.

Com $M$ selecionado, o que vai acontecer é o seguinte:

se o nó $M$ puder ser expandido, vamos adicionar um novo filho a ele. Seu novo filho será simulado e o resultado da simulação será retropropagado para $M$ (assim como para seus antecessores). Efetivamente, estaremos fazendo uma segunda amostragem aleatória para o nó $M$ .
se o nó $M$ não puder ser expandido, então ele é um nó terminal - e não tem como amostrar um resultado possível a partir dele, porque ele já é um resultado. Simplesmente retropropagamos o valor dele, dando mais amostragens aleatórias para seus antecessores.

Independente de qual a natureza do nó $M$ , a verdade é que se nessa segunda amostragem aleatória ele também der "vitória", ele continua sendo um bom indício - e seu UCT continuará alto, e ele continuará sendo selecionado e amostrado. Em contrapartida, se começarmos a gerar diversas amostras aleatórias de "derrota" para $M$ e seus filhos, seu UCT diminuirá e ele começará a ser "esquecido".

Então no fim das contas, acabamos num esquema em que, indiretamente e inevitavelmente, os nós mais promissores acabarão sendo amostrados milhares de vezes, depois de milhares de iterações. Não precisamos fazer os milhares de amostras na hora da inicialização porque o próprio processo de construção da árvore acaba fornecendo isso pra gente!

E essa é basicamente a etapa de simulação: gerar uma amostra aleatória para um nó, seja ele recém-expandido (vindo da etapa de expansão) ou terminal (vindo da etapa de seleção). Ufa!

4. retropropagação

"O que o resultado dessa simulação significa pro resto da árvore?"

Como você já deve imaginar, a etapa de retropropagação é responsável por propagar os resultados de uma simulação para os antecessores do nó simulado. Portanto:

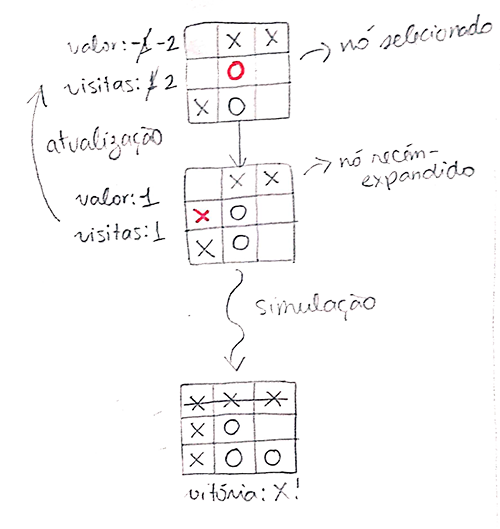
Isso significa iterar por todos os nós descendentes do nó recém-expandido, e fazer duas atualizações:

o atributo visitas deve ser incrementado em $1$ ;
o atributo valor deve ser incrementado de acordo com o resultado da simulação (p. ex.: vitória +1, derrota -1, empate 0)

É importante destacar um detalhe. Lembre-se da nossa discussão anterior sobre a modelagem com dois jogadores. Se a simulação terminou em vitória para o jogador X, os antepassados relativos ao jogador X aumentarão o seu valor, enquanto os relativos ao jogador O irão diminuir o seu valor (já que o jogador O perde com aquele resultado).

fim da iteração

E é isso! Depois dessas 4 etapas, a iteração do algoritmo chegou ao fim. Recapitulando, o que fizemos foi o seguinte:

seleção - percorrer a árvore buscando os nós de maior UCT, até chegar em um nó da árvore ainda não-expandido (ou um nó terminal).
expansão - se chegarmos em um nó que ainda pode ser expandido, adicionamos as possíveis expansões à árvore (talvez uma de cada vez, talvez todas ao mesmo tempo).
simulação - simulamos um jogo a partir daquele ponto até obtermos um resultado. Assim preenchemos o valor do nó selecionado.
retropropagação - atualizamos os antepassados do nó simulado de acordo com o resultado da simulação.

Obviamente, fazer uma única iteração não é bom o suficiente - o ideal é fazermos milhares, para que possamos obter a melhor decisão possível. Como dissemos anteriormente, temos que estabelecer algum critério de parada (p. ex.: número de iterações), e assim que esse critério for atingido, consideramos nossa árvore como "finalizada".

Mas espera. Isso tudo porque queríamos buscar a melhor decisão a ser tomada? Como extraímos essa decisão a partir da árvore "finalizada"?

Essa é a parte mais fácil! Nós sabemos que a melhor decisão será um nó dentre os filhos da raiz. Mas qual? Dois critérios possíveis são:

o nó de maior UCT;
o nó com mais visitas.

Ambos os critérios tem bons argumentos: o nó de maior UCT é o mais promissor, e o nó com mais visitas é aquele cuja estimativa é mais próxima do valor real (porque ele foi mais simulado). Na prática é uma decisão de implementação. Na nossa implementação, estamos utilizando esse segundo critério. Basta aplicá-lo para encontrar a melhor decisão a ser tomada!

E falando da nossa implementação, agora é um bom momento pra voltar a falar dela! A página está aqui, e seria uma boa ideia tentar observar como a árvore se comporta nas seguintes situações:

uma situação em que o algoritmo pode vencer, se tomar a decisão certa;
uma situação em que você está prestes a vencer, e o algoritmo deve te bloquear o mais rápido possível!
uma situação em que o algoritmo não tem como vencer (boa sorte com isso...)

E é isso. Eu vou ficar por aqui. Divirta-se!

bibliografia

Browne, Cameron B., et al. "A survey of monte carlo tree search methods." IEEE Transactions on Computational Intelligence and AI in games 4.1 (2012): 1-43.
Kocsis, Levente, and Csaba Szepesvári. "Bandit based monte-carlo planning." European conference on machine learning. Springer, Berlin, Heidelberg, 2006.